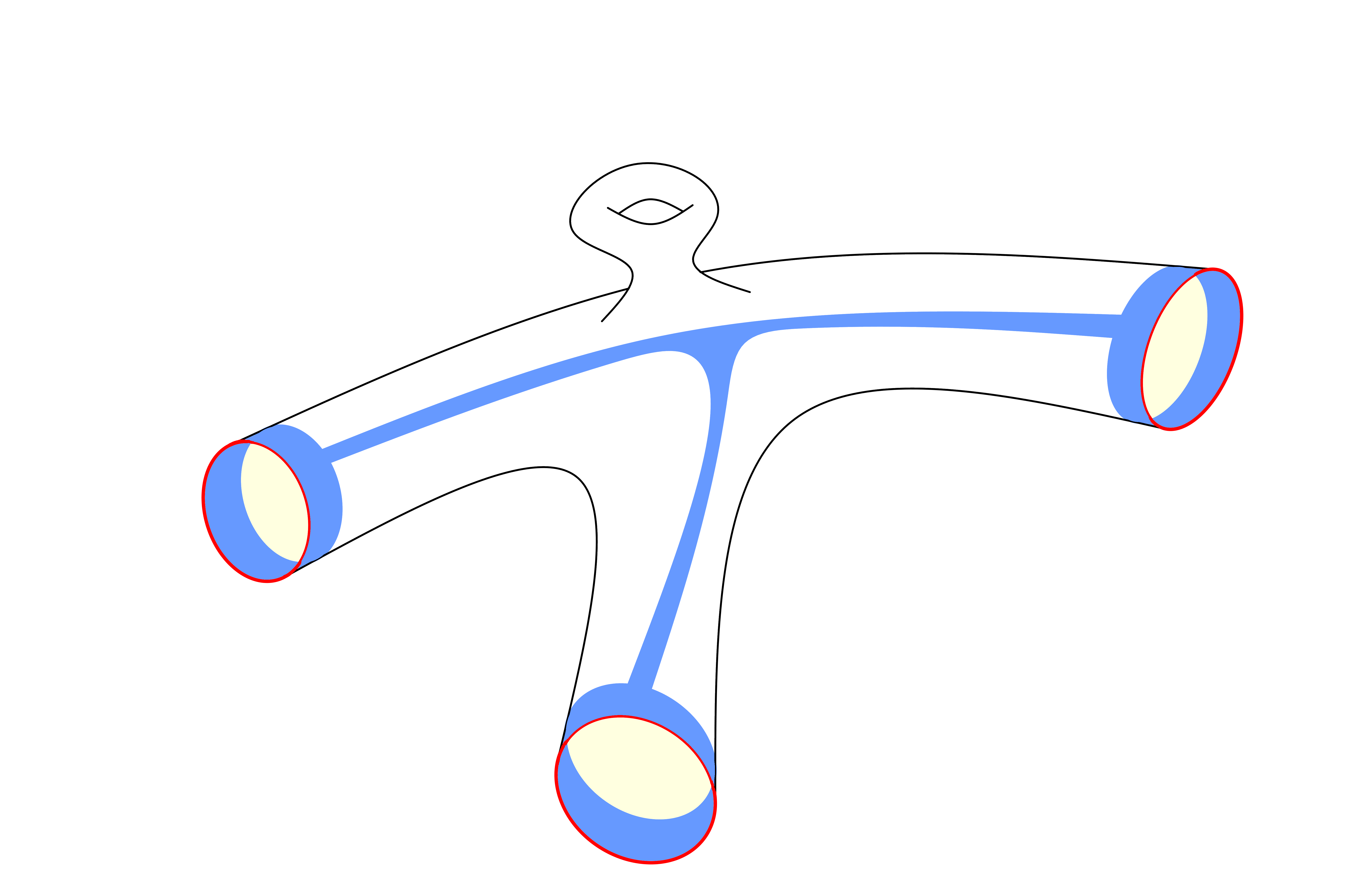
Broadly, my academic interests were in Riemannian geometry and geometric analysis. More specifically, my background and training was in spectral geometry, where one is interested in the interplay between the geometry of a manifold and the spectrum of some geometrically motivated differential operator (e.g. the Laplace-Beltrami operator). In my PhD thesis I investigated the singularities of the wave trace on lens spaces and flat manifolds (the so-called Poisson relation). After getting my PhD in Mathematics at Dartmouth College, I spent a year at Université Laval, where I was a CRM Postdoctoral Fellow in the Department of Mathematics. At Laval I worked with Alexandre Girouard on questions related to the Steklov spectrum. After Laval, I did another post-doc at the University of Michigan. At Michigan, I branched out to investigate questions motivated by mathematical physics, fluid mechanics and numerical analysis.
- Publications
- Spectral Multiplicity and Nodal Domains of Torus-Invariant Metrics (with Chris Judge, Samuel Lin and Craig Sutton, 2023)
- On branched minimal immersions of surfaces by first eigenfunctions (with Misha Karpukhin and Vladimir Medvedev, 2019)
- Large spectral gaps for Steklov eigenvalues under volume constraints and under localized conformal deformations (with Alexandre Girouard, 2018)
- From the Boltzmann Equation to Fluid Mechanics on a Manifold (with Peter Love, 2011)
- Lattice Gas Simulations of Dynamical Geometry in Two Dimensions (with Anna Klales, Zachary Needell, David A. Meyer and Peter Love, 2010)
- Preprints/Unpublished work
- Semi-classical incarnations of the Inverse Spectral Method: The inverse spectral method has been used to study, among other things, the continuous limit of the Toda lattice and the dispersionless limit of the KdV equation. Alejandro Uribe and I investigated an analog of the inverse spectral method for a class of "tri-diagonal" Toeplitz operators obtained from quantizing the 2-sphere. The work was inspired by this article. Our preliminary results can be found here.
- Point vortex dynamics: Point vortices provide a useful toy model for helping to understand vorticity in fluid flows. They also have many connections to other areas of mathematics, e.g. dynamical systems, Hamiltonian dynamics and potential theory. Jörn Zimmerling and I mentored three undergraduates in a Lab of Geometry project where we investigated the dynamics of the vortices whose motion is confined to a curved surface (like a sphere or a torus). The video to the right is a simulation of three planar vortices in an equilateral triangle configuration where the vortices are known to steadily rotate around the center of the triangle.
- On the Poisson relation for flat and spherical space forms (2016)
- Previous Teaching
- Math 316 (Differential Equations) Winter 2019 - Primary Instructor at University of Michigan
- Math 217 (Linear Algebra) Fall 2019 - Instructor at University of Michigan
- Math 217 (Linear Algebra) Winter 2019 - Instructor at University of Michigan
- Math 216 (Introduction to Differential Equations) Fall 2018 - Instructor at University of Michigan
- Math 217 (Linear Algebra) Winter 2018 - Instructor at University of Michigan
- Math 115 (Calc I) Fall 2017 - Instructor at University of Michigan
- Math 20 (Introduction to Probability) Summer 2015 - Primary Instructor at Dartmouth College
- Math 8 (Calc I) Fall 2014 - Instructor at Dartmouth College